

APPLICATION OF THE LETTER SERIAL CORRELATION TEST TO THE VOYNICH MANUSCRIPT
Part 2. Discussion of experimental data and possible interpretation of the manuscript's nature
by Mark Perakh
posted on July 2, 1999


CONTENTS
Preface
4. Specific LSC sums and LSC densities in VMS
5. Discussion of experimental data
1. Meaningful text or gibberish?
a) Total LSC sums, densities and specific sums
b) Uniformity of characters frequency distribution
(i) Characters frequency distribution comparison assuming that all characters in VMS are letters
(ii) Letter frequency distribution comparison assuming that 10 least frequent characters represent numerals.
(iii) Ranking VMS on entropy scale
2. One or two languages in VMS?
(a) Similarity of "VMS A vs VMS B" to the regularities in other meaningful texts
(b) Two sets of characters in VMS
(c) Abbreviated text in VMS A?
(d) Vowels vs consonants in VMS
6. CONCLUSION
7. REFERENCES
PREFACE
In part 1 of this paper the basic experimental data were shown obtained by applying Letter Serial Correlation (LSC) test [7,8,10-13] to the Voynich manuscript (VMS). In this part, the discussion of those data will be presented, aimed at producing certain hypothesis in regard to the nature of the Voynich manuscript as a whole, and of its parts A and B. For that discussion, some additional experimental data, both of LSC and of some other measurements, will be utilized. Since both parts 1 and 2 constitute essentially one paper, the sections, graphs, and tables are numbered consecutively throughout both parts 1 and 2. To facilitate the navigation through both parts, hyperlinks are supplied where appropriate.
Understanding the following material requires familiarity with the LSC effect and its features, as they have been laid out and discussed in [7,8,10,11,12,13].
4. Specific LSC sums and LSC densities in VMS
In order to better compare the behavior of the text as a whole and of its parts written in "languages" A and B, a quantity more convenient than the LSC sum per se would be specific LSC sum [12] calculated by means of dividing the measured LSC sums by the actual lengths L* of the text. If the text’s nominal length L, measured in the number of letters, is divisible by k - the number of "chunks" into which the text is divided for measuring LSC sum, then L*=L. If, though L/k is not an integer, then L* is the truncated length of the text, from which the incomplete, last chunk is cast off.
The use of specific sums eliminates the discrepancies in absolute values of sums to be compared and enables us to view the specific LSC sums for all three versions, in one graph, shown in Fig. 5, where the red curve relates to VMS-A, the green curve, to VMS-B, and the blue one, to VMS as a whole.
To further investigate the behavior of the Voynich text, also the Letter Serial Correlation densities [7] have been calculated. In fig. 6, 7 and 8, the log-log plots are shown for LSC densities for parts of VMS written in languages A and B, and for the VMS as a whole.
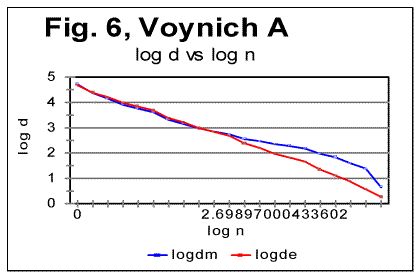
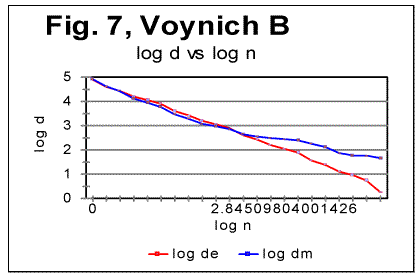
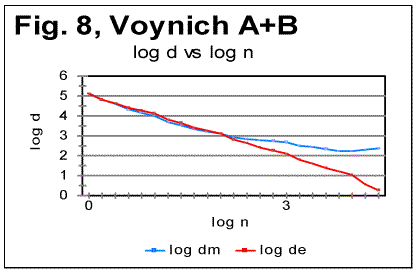
5. Discussion of experimental data
Let us analyze the data represented in Figs 1-4 (in Part 1 of this paper), Figs 5-8 (above) and in Table 1 (in Part 1).
1) Meaningful text or gibberish?
a) Total LSC sums, densities and specific sums
The graphs in Figs 1-4 have the typical shape of those obtained for meaningful texts in natural languages we have studied so far (the total of 12 languages, comprising 69 different texts - see [10,11,12,13]). On these graphs, we observe all the standard features seen on such graphs for meaningful texts, namely the Downcross Point, the Primary Minimum Point, and the Upcross Point [10].
Furthermore, these graphs clearly differ, in a substantial way, from those graphs we obtained for texts randomized by permuting letters of original meaningful texts - see [8]. None of the above characteristic points are seen on the LSC curves for randomized texts.
The graphs in Figs 1-4 differ clearly and quite substantially also from the graphs for the artificially created "nearly-zero-entropy text"(ZET) [11] and for the artificially created Low-entropy texts LET-1 and LET-2 [11]. The LSC curves for the ZET, LET-1 and LET-2 have completely different overall shapes and do not show any characteristic points that are present on LSC curves for meaningful texts.
In [11] was shown, however, that an artificially created gibberish can display the behavior which at a first glance seems to be similar to meaningful texts. However, the more detailed review of those tests for the artificially created gibberish showed distinctive differences if compared with the meaningful texts. Then only one type of text which was found to display a behavior similar to meaningful texts, was a text [12,13] created by permuting words within verses (in the Book of Genesis in Hebrew) without permuting verses themselves. We will refer to it as W/V text.
Since we know precisely the behavior of LSC sums for a)"nearly-zero-entropy" text, b) for letter- randomized and word-randomized texts, c) for meaningful texts, d) for an artificially created gibberish, and e) for W/V text, we can note that both A and B components of VMS behave, in regard to LSC sums, like either c), or e), but quite differently from a) , b), and d).
We can note also that for VMS the values of characteristic points of LSC are very close to those found for many of the natural languages we studied [10,11]. Indeed, the location of the Downcross Point (between n=2 and n=3), and of the Primary Minimum Point (at n=30) for "language" B are exactly the same as they are, for example, for the English text of Moby Dick, whereas the location of the Upcross Point for "language" B (at n=150) is the same as, for example, for most of the texts in Hebrew we studied, as well as for many English text stripped of vowels. However, for some meaningless texts, namely for the artificially created gibberish and for W/V text, all characteristic points mentioned were also found to be in the same range.
As for "language" A, the location of Downcross Point (at n between 1 and 2) and of the Primary Minimum Point (at n=8) are almost the same as, for example, for the English text of Moby Dick, stripped of all consonants (the Upcross Point for "language" A is at n=62, which is lower than for other languages we studied, either for all-letter versions, or for versions stripped of either vowels or of consonants).
The data for the Letter Serial Correlation density for "languages" A and B, shown in Figs. 6-8, also display a behavior typical of either the meaningful texts in the natural languages we studied [10,12,13] or in W/V text [12,13]. Furthermore, these curves differ substantially from those obtained both for truly randomized texts [8] and for the artificial "zero-entropy text," "low-entropy text" and the artificially created gibberish [12,13]. Indeed, the log-log density curves for VMS display the same characteristic deviation of the curve for the measured sum Sm from that for the expected sum Se, which deviation starts close to the Primary Minimum Point (PMP). On the other hand, the density log-log curves for truly randomized texts [8] practically coincide for both the expected and the measured LSC densities, in the entire range of chunk's sizes. The same situation was observed for V-shuffled text of Genesis [12,13]. Also, density log-log curves for ZET, LET-1, and LET-2 [12,13] have shapes completely different from those for both the meaningful texts and the VMS.
Hence, on the base of the data described in [10,12,13] and the LSC test on VMS, we may assert what VMS is not: VMS is not a truly random collection of symbols.
As to what it is, there are alternatives, to wit: 1) It is a meaningful text, and 2) it is a gibberish deliberately created either by randomly writing symbols or by shuffling the words within meaningful verses (however unlikely the last alternative is). Such a gibberish must though be quite different from the one I artificially created and described in [12,13] . While creating the artificial gibberish, my tendency was to achieve a letter distribution as close to the truly random one as possible. Whereas I did not succeed fully in that task, I succeeded partially, as the artificial gibberish had certain characteristics making it similar to some extent to a truly random text [12,13]. On the other hand, it cannot be excluded that the creator (or creators) of VMS had the opposite intention, namely to imitate a meaningful text. If this was the case, then VMS might be a gibberish deliberately imbued with characteristics of a meaningful text. Of course such a hypothesis would encounter its own difficulties as it is hard to figure out how such a task could be performed. Nevertheless, the data we discussed so far do not contradict that hypothesis, however strange it may sound. To make the choice between the alternatives 1) and 2), we will have to analyze more in detail both the subtle features of LSC in VMS and some other aspects of VMS text's behavior.
b) Uniformity of the characters frequency distribution
A feature which, besides LSC, characterizes texts, is the uniformity of the letter frequency distribution in a text. The quantity that estimates the uniformity of a distribution ("spread" in the parlance of Mathematical Statistics) is Coefficient of Variation (CV). The definition ov CV was given in [13]. The larger is that coefficient for a text, the less uniform is its letter frequency distribution. The value ov CV for artificial gibberish was found to be smaller than for any of 69 meaningful texts in 12 languages we explored. It means that the artificial gibberish was found to display a considerably better uniformity of letter frequency distribution than any of the 69 meaningful texts in 12 languages we explored. Therefore, it seemed desirable to calculate CV for both VMS-A and VMS-B and to compare it to meaningful texts and to the artificial gibberish described in [12,13].
While comparing the letter frequency distribution for VMS to that for the previously tested meaningful texts, we have to take into account that in the previously tested texts we accounted only for letters, omitting numerals, which anyway happened very rarely if at all in those texts (in particular, in Hebrew texts numerals are represented by regular letters). VMS though is different in that some of its characters may represent numerals, as distinctive from letters. Therefore, I chose to perform the comparison of characters frequency distribution for two extreme assumptions. One assumption was that all characters in VMS represent only letters. The other, opposite, extreme assumption was that some 10 characters in VMS represent numerals from 0 to 9. While working under the second extreme assumption, I assumed additionally that characters representing numerals are those which are the least frequent in VMS texts. While such an assumption may be justifiably considered somehow arbitrary, it provided a way, as it will be explained later in this paper, to evaluate the actual behavior of the letter frequency distribution in VMS texts.
(i) Letter frequency distribution comparison assuming that all characters in VMS are letters
In Figs. 9 and 10 the histograms of characters frequency distribution are shown for Voynich-A and Voynich- B. In Fig. 11, for comparison, the histogram for the text of Moby Dick in English is shown, and in Fig. 12 the data for the artificially created gibberish are presented.
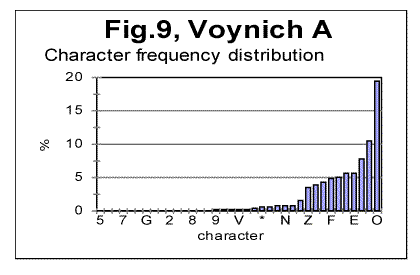
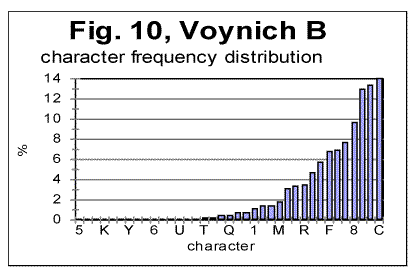
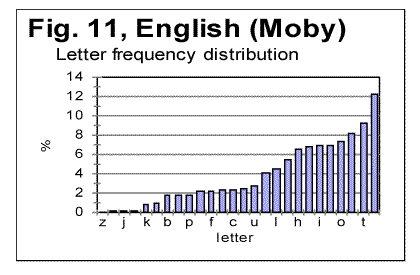
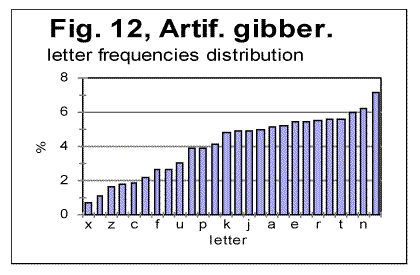
As can be seen from Figs. 9-12, assuming that all characters in VMS are letters, the distribution of characters frequencies in both Voynich-A and Voynich-B is sharply non-uniform, its uniformity being obviously substantially below that in the meaningful English texts, and even more below the artificially created gibberish. To give this visual impression a quantitative measure, I calculated the Coefficient of Variation, denoted CV and measuring spread of a distribution (see its definition in [13]) for a number of meaningful texts, and compared it with both Voynich-A and-B, and with the artificial gibberish described in [12]. The results are gathered in Table 2. The smaller is the value of CV, the more uniform is the characters frequency distribution.
Table 2. Coefficient of Variation for various texts
Text |
CV |
| VMS A (if all characters are letters) | 1.84 |
| VMS B (if all characters are letters) | 1.487 |
Czech |
1.046 |
German |
1.036 |
Spanish |
1.015 |
Greek |
0.933 |
Finnish |
0.92 |
Latin |
0.894 |
Russian |
0.888 |
English, no vowels |
0.866 |
Italian |
0.86 |
English |
0.834 |
Spanish, no vowels |
0.833 |
Yiddish (in Latin letters) |
0.811 |
Czech, no consonants |
0.807 |
Latin, no vowels |
0.794 |
Hebrew |
0.749 |
Artificial gibberish |
0.425 |
As can be seen from Table 2, the artificial gibberish shows the minimum value of the Coefficient of Variation CV, among all the tested texts, while both Voynich-A and Voynich-B in which all characters are assumed to be letters, have the maximum value of CV among all those tested texts, i.e the letter frequencies distributions for both VMS-A and VMS-B are least uniform among all tested texts.
If all characters in VMS are indeed letters, then the data shown in Table 2 render quite unlikely the hypothesis that either Voynich-A or Voynich-B is a highly disordered gibberish like the one I artificially created as described in [12]. Of course, it does not indicate that VMS-A or VMS-B is necessarily a meaningful text. Either of them still can be a gibberish, but of a type different from the artificial one we described in [12]. While creating the artificial gibberish in [12] I aimed at creating a text which would be as close to a truly random one as humanly possible. I did not fully succeed in that effort, as it can be seen from the fact that for my gibberish CV>0, while for a truly random text it would be CV=0. I succeeded though to some extent since the uniformity for my gibberish turned out to be better than for any meaningful text tested. What follows from the results in Table 2 is, that if VMS is a gibberish, then its creator (or creators) deliberately favored some characters at the expense of some other characters, in order to avoid a very uniform character frequency distribution, and hence to imitate in this way a meaningful text, and that he, she, or they happened to be overzealous in their effort.
(ii) Character frequency distribution in VMS assuming that 10 least frequent characters represent numerals.
Under this extreme assumption, we exclude from each of the histograms in Figs. 9 and 10, ten least frequent characters assuming they represent numerals. In this case the uniformity of letter frequency distribution in VMS texts improves, but not very dramatically, the values of Coefficient of Variation becoming, for VMS-B, CV=1.67, and for VMS-A, CV=1.396, hence still being above the values of CV for any previously tested meaningful text. Therefore, the conclusion made at the end of the preceding paragraph remains in force also under the second extreme assumption.
Having thus excluded a number of possible versions of VMS text's type, we have now reduced the choice between the possible types of texts constituting VMS to only two possibilities, of which the second one, albeit mentioned earlier in this paper, can be slightly modified now, to wit: 1) A meaningful text, and 2) A deliberately created gibberish with a rather high degree of organization.
If we adhere to choice #1, we will have to explain why the non-uniformity of letter frequency distribution in VMS is distinctively larger than in any meaningful text we studied in 12 languages. Of course, if we choose option #2, this question will be moot, as the extreme non-uniformity can easily be a result of an overzealous deliberate effort.
(iii) Ranking VMS on the entropy scale
There is a wide range of possible texts in regard to their entropy. This range extends from the zero-entropy text (for example a "text" consisting of L identical letters) to perfectlly random "texts" which can be created by randomly placing letter in the "text" in accordance with computer-generated random numbers (the maximum entropy of such texts is Smax=log2 z bits per letter, where z is the number of available letter-tokens in the alphabet). Somewhere within the above range there is a sub-range of meaningful texts, whose entropy is larger than that for the highly-ordered artificial conglomerates of letters (like the "nearly-zero-entropy text" explored in [12,13]), but smaller than for randomized texts (such as, for example, those created by permuting the letters of an original meaningful text - see [8]). A scale of entropy ranks for various texts was suggested in [13]. In that scale various texts were ranked in accordance with a quantity we named Combined Empirical Entropy Estimator (CEEE) and which was an empirical ("phenomenological") coefficient combining the observed characteristics of LSC (such as the Depth of Minimum, DOM, and position - nmin - of the Primary Minimum Point on the LSC sum curve) with an ad-hoc characteristic of uniformity of letter frequency distribution I named Coefficient of Uniformity (CU) . I will reproduce here the table of CEEE for various texts, now including into it also the data for Voynich-A and Voynich-B, calculated under the first extreme assumption, namely that all characters in VMS are letters. These data are shown in Table 3.
Table 3, Combined Empirical Entropy Estimator (CEEE) for various texts
Text |
CEEE |
Perfectly random |
1.0000 |
Letters-permuted |
0.2000 |
Words-permuted |
0.1365 |
Verses permuted |
0.0755 |
Artificial gibberish |
0.0697 |
Words-in-verses permuted |
0.0683 |
Hebrew |
0.0628 |
Russian |
0.0481 |
Yiddish (in Latin letters) |
0.0433 |
German, no-vowels |
0.0387 |
Greek |
0.0301 |
| Voynich A | 0.0251 |
Spanish |
0.0230 |
Czech |
0.0200 |
Latin, no-vowels |
0.0189 |
English |
0.0155 |
Latin all-letters |
0.0128 |
German, all-letters |
0.0120 |
Italian, all-letters |
0.0078 |
Italian, no-consonants |
0.0048 |
| Voynich B | 0.0047 |
Finnish |
0.0033 |
Artificial zero-entropy text (estimate) |
0.00001 |
As we can see from Table 3, despite VMS being highly non-uniform in its character frequency distribution, the overall empirical criterion of their entropy places both Voynich-A and Voynich-B within the range of meaningful texts. We see also that the entropy of VMS-A is considerably larger then that for VMS-B (this observation will be discussed in one of the following sections).
If we accept the second extreme assumption, namely that 10 least frequent characters represent numerals, the values of CEEE for both VMS-A and-B increase, but they still remain within the range for meaningful texts.
To summerize all the data presented so far we can rather confidently assert the following: 1) VMS is not a truly random collection of symbols. 2) VMS is not a deliberately created quasi-random text, 3) VMS was not created by permuting either letters, or words, or paragraphs, etc, of a meaningful text.
There seem to be two possible interpretation of the data presented so far, both discussed already in this paper. One is that VMS is indeed a meaningful text in some so far unidentified language, which is charaterized by a sharply non-uniform distribution of letters frequencies. The second possible interpretation, also already discussed before in this paper, is again that VMS is a deliberately created, highly organized gibberish, whose creators managed to imitate to a considerable extent the appearance and features of a meaningful text, but erred in overusing some characters at the expense of some others. The additional discussion of these alternatives will be offered in Conclusion.
Let us see now if we can shed some more light on the VMS puzzle by considering the similarities and differences between its A and B parts.
2. One or two languages?
a) Similarity of "VMS-A vs VMS-B" to the regularities in other (meaningful) texts
One of the immediately evident differences between VMS-A and VMS-B texts is that the average length of a word in VMS-B is by about 35% larger than it is in VMS-A. Another difference between the two versions of VMS is that there are several words that are very common inVMS-A but happen rarely in VMS-B (for example, one such word is represented by characters 8AM) and, also, there are words which are common in B but absent in A (for examples words represented by characters SC89 and ZC89).
To analyze the differences and similarities between Voynich-A and Voynich-B, as they are evident via LSC test, we have to assume that VMS is a meaningful text. Indeed, if VMS is a deliberatelly created gibberish that imitates a meaningful text, the difference between two versions of such a gibberish would be a result of arbitrarily chosen variations in its makeup, and as such would be of no meaning.
Let us take another look at the graphs for total LSC sums (Figs. 1-4) and specific LSC sums (Fig. 5). What seems immediately obvious, is an analogy between the changes in LSC curves, observed when some meaningful all-letters text in a natural language is replaced with a no-vowels text, on the one hand, and when Voynich-B is compared toVoynich-A, on the other hand.
Many examples of all-letters and no-vowels versions of the same text in natural languages were discussed in [10,11] and [12,13]. These examples show that as either vowels or consonants are removed from a meaningful text, two things invariably occur, namely: 1) The Primary Minimum Point shifts to lower values of chunk's size n (it is usually accompanied by a collateral effect, which is a similar shift of the Upcross Point to lower n ). 2) The Depth of Minimum decreases in no-vowels (and in no-consonants) versions as compared to all-letters texts. For example, in the all-letters English text of Moby Dick, PMP is at n=50, in its no-vowels version it is at n=30, and in its no-consonants version it is at about n=8. The Depth of Minimum, which is DOM=0.161 for the all-letters version, becomes DOM=0.11 for the no-vowels version, etc.
A very similar effect is observed for VMS. The location of PMP in Voynich-A (about n=8) is at the substantially lower n than it is in Voynich-B (n=30). The depth of minimum for Voynich-B is DOM=0.312, while for Voynich-A it drops to DOM=0.228.
Look now at the specific LSC sums in VMS-A and VMS-B (Fig. 5). We have to remember that A and B are two different texts, whereas the all-letters and no-vowels versions of a meaningful text are always two versions of the same text. Nevertheless, there is a substantial similarity between two cases, namely the relative configuration of specific LSC sums for all-letters vs. no-vowels texts, on the one hand, and relative configuration of specific LSC sums for Voynich-A vs Voynich-B, on the other. In all meaningfuil texts that we tested, at small n the specific LSC sum for the no-vowels version runs below that for the all-letters version. At a certain value of n=p, the specific LSC sum for the no-vowels version grows above the sum for the all-letters version. In [11] we offered an interpretation of the described behavior of specific LSC sums. As can be seen from Fig. 5, Voynich-A and -B behave in a very similar way. Indeed, at small n the specific LSC sum for Voynich-A runs below the curve for Voynich-B, but at n which is about n=p=4, the curve for A crosses that for B, and at larger n the specific LSC sum for A runs above that for B.
There are some minor differences between the behaviors of specific LSC sums for the languages we studied previously, on the one hand, and VMS on the other. One such difference is the very close values of specific sums for VMS-A and VMS-B at n=1, while for the meaningful texts we studied, usually at n=1 the sum for no-vowels text is distinctively smaller than it is for the all-letters text. This difference can be easily understood though, as it will be discussed a little later in this paper. Another difference is that both curves for A and B intersect with the curve for the total VMS text almost precisely at the same n. However, this peculiarity of the specific LSC sums for VMS can be easily understood as well, if we take into account that in the meaningful texts which we tested, vowels and consonants constitute an intimate mix, whereas in VMS, parts A and B are mixed in rather large blocks of text.
Indeed, the total VMS text is the sum of A and B parts, which are intermixed in rather large blocks of texts A and B. If the LSC sum for the full text is ST, and for parts A and B the sums are SA and SB, then the specific sums are ST/LT, SA/LA and SB/LB.. Obviously ST/LT=(SA+SB)/LT. Now, if for a certain n, SA/LA=SB/LB, then, if LA=LB (approximately) then (SA+SB)/LT =SA/LA= SB/LB (approximately). The last equation holds better if LA=LB exactly. So, for the three curves to intersect almost at the same point, two conditions must be met, to wit: a) LA=LB (approximately). b) The clusters of both texts A and B whose mix forms the total text must be relatively large, i.e. larger than the size of a chunk, so that their mixing does not destroy the structure of individual chunks. For an intimate mix, such as, for example, the mix of vowels and consonants in a meaningful text, condition b) does not hold, hence the separate curves of S/L , using sums SV for vowels and SC for consonants, do not intersect at the same point where they intersect each separately with the curve for the all-letters text. If only vowels are plucked out from a chunk, the structure of that chunk changes. Therefore the chunks, which are made up only of vowels or only of consonants, have structures different from the structure (composition) of chunks for the all-letters text, hence, unlike the case of VMS, the measured sum Sm for them are different, and (SV+SC )/LT is not equal SV/LV .
Since the observed minor differences between specific LSC sums for the two cases, one of no-vowels vs all-letters versions of meaningful texts, and the other of Voynich-A vs Voynich-B, have a rather simple and natural explanation, we have to note the otherwise considerable similarity between the two cases in question.
To further investigate this similarity, let us consider again the histograms of character frequency distributions for VMS and for some previously tested texts.
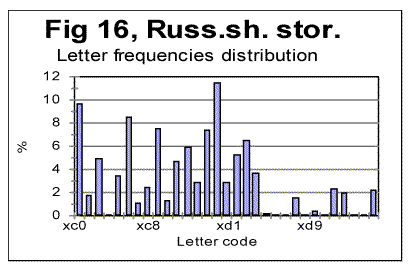
Unlike in previous histograms, where letter frequencies were arranged in ascending orders, now we will arrange them in the alphabetical order of letters, to easier see the possible differences and similarities between histograms. In Figs. 13 and 14 letter frequencies are compared for two quite different languages, German and English. Figs. 13 and 15 show the histograms for German and Yiddish, the latter represented by Latin characters. Of course, Yiddish is much closer to German than English, especially since it is represented here by Latin characters. Fig 16 shows the letter frequency distribution for Russian text which is rather different from the other three texts. The letter codes for Russian are shown instead of letters because we could not print the Cyrillic characters on the abscissa of that graph. These codes are arranged in alphabetical order, so that the leftmost peak corresponds to letter A, and the highest peak (fifteenth from the left) corresponds to letter O, which is the most frequent letter in Russian texts.
It is easy to see that there is a distinctively larger difference in letter distribution pattern between, say English and German, or between English and Russian, than it is between German and Yiddish. For example, the most frequent letter in English is E followed by T. In German and Yiddish the most frequent letter is also E, but the following one is N rather than T. In Russian two most frequent letters are O followed by A, etc.
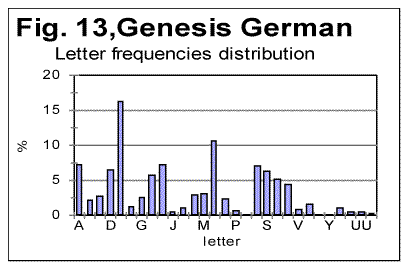
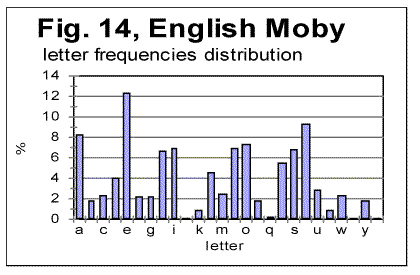
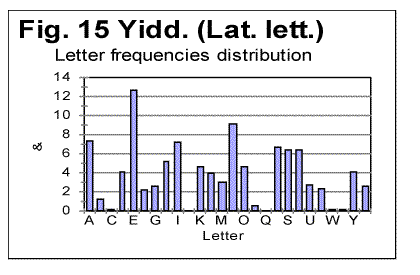
Still, there are some rather easily observed differences in letter frequency distribution between German and Yiddish as well, which are better evident when the low-frequency letters are compared, such as V or W, etc.
Now let us compare letter frequency distributions for two texts in the same language, one of them the all-letters text, and the other the same text stripped of vowels. These two histograms are shown in Figs. 17 and 18.
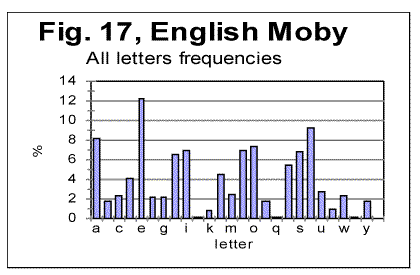
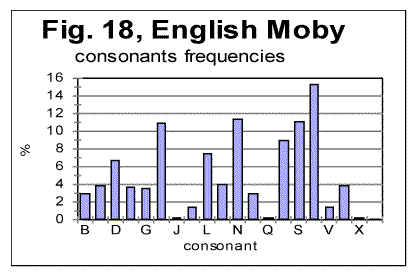
As it could be expected, all peaks for consonants observed in Fig. 17, remain in their places in Fig 18, while the peaks for vowels disappear, and the height of consonants peaks increases, as in the absence of vowels the fraction of each consonant in the text increases proportionally. Generally speaking, the shapes of the histograms in Figs 17 and 18 are much closer to each other than they are even for such close languages as German and Yiddish, not to mention such different languages as English and Russian. One feature observed in Figs. 17 and 18, which is of interest for us, is that the ascending order of frequencies for consonants is identical in both above distributions. For example, the most frequent consonants, in the descending order, in both histograms in Figs. 17 and 18, are T, N, S, H etc. Of course, this is a trivial observation, but it is useful for the further discusssion.
Finally, let us look at the histograms for Voynich-A and Voynich-B, shown in Figs. 19 and 20. These histograms pertain to the first extreme assumption, namely that all characters in VMS are letters.
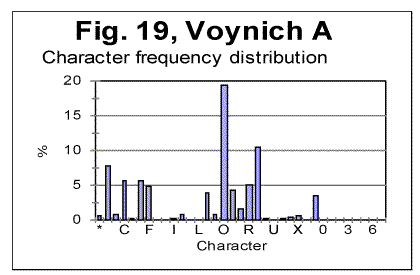
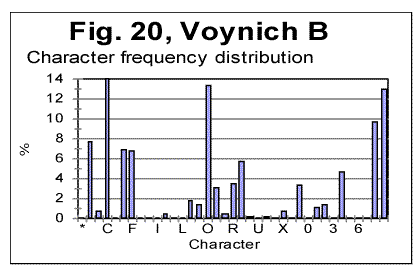
We can see from Figs. 19 and 20, that the histograms for Voynich-A and-B have many similarities. There are only two characters which are present in VMS-B but are absent in VMS-A, namely characters 1 and 5. On the other hand, there are many characters whose frequency is drastically lower in A than it is in B, for example characters C, 4, etc. Overall, the characters in VMS can be divided into two groups, one consisting of characters whose frequency is larger in B than it is in A (we will refer to these characters as V-characters) and others whose frequency is larger in A than it is in B (to be referred to as C-characters). If we consider the separate distributions of V-characters and of C-characters, they turn out to be alsmost identical in VMS-A and VMS-B, in the sense that the order of frequencies in each of the two groups of characters is almost the same in VMS-A and VMS-B, as it will be shown below.
In Table 4, all characters that appear in VMS are listed, with their frequencies both in A and B. In the rightmost column it is indicated where this or that character is more frequent, in VMS-A or in VMS-B.
Table 4. Comparison of frequencies of characters in Voynich A and Voynich B
Character |
Frequency in A, % |
Frequency in B, % |
Where it is more frequent |
| * | 0.529 |
0.108 |
A |
A |
7.868 |
7.760 |
A |
B |
0.755 |
0.771 |
B |
C |
5.621 |
13.991 |
B |
D |
0.295 |
0.060 |
B |
E |
5.707 |
6.930 |
B |
F |
4.808 |
6.836 |
B |
G |
0.015 |
0.039 |
B |
H |
0.015 |
0.007 |
A |
I |
0.212 |
0.041 |
A |
J |
0.733 |
0.395 |
A |
K |
0.042 |
0.011 |
A |
L |
0.015 |
0.007 |
A |
M |
3.834 |
1.812 |
A |
N |
0.744 |
1.340 |
B |
O |
19.321 |
13.415 |
A |
P |
4.355 |
3.117 |
A |
Q |
1.628 |
0.443 |
A |
R |
4.975 |
3.478 |
A |
S |
10.588 |
5.712 |
A |
T |
0.212 |
0.211 |
A |
U |
0.087 |
0.089 |
B |
V |
0.230 |
0.236 |
B |
W |
0.344 |
0.085 |
A |
X |
0.627 |
0.716 |
B |
Y |
0.079 |
0.039 |
A |
Z |
3.441 |
3.402 |
A |
0 |
0.0003 |
0.018 |
B |
1 |
0.000 |
1.106 |
B |
2 |
0.0182 |
1.411 |
B |
3 |
0.0013 |
0.110 |
B |
4 |
0.0238 |
4.652 |
B |
5 |
0.0000 |
0.005 |
B |
6 |
0.0014 |
0.055 |
B |
7 |
0.0005 |
0.011 |
B |
8 |
0.0764 |
9.694 |
B |
9 |
0.1072 |
12.993 |
B |
b) Two sets of characters in VMS
Now, as the next step, let us extract from Table 4 all those characters (which we will refer to as C-characters) whose frequency in VMS-A is larger then it is in VMS-B and compare the frequency distributions of those C-characters in Voynich-A and Voynich-B. These distributions are shown in Tables 5 and 6.
Table 5. C-characters frequencies in Table 6. C-characters frequencies in VMS-A VMS-B
| Table 5 | Table 6 | |||
| Character | Frequency in V.A, % | Character | Frequency in V. B, % | |
L |
0.015 |
L |
0.007 |
|
H |
0.015 |
H |
0.007 |
|
K |
0.042 |
K |
0.011 |
|
Y |
0.079 |
Y |
0.039 |
|
T |
0.212 |
I |
0.041 |
|
I |
0.212 |
D |
0.060 |
|
D |
0.295 |
W |
0.085 |
|
W |
0.344 |
* |
0.108 |
|
* |
0.529 |
T |
0.211 |
|
J |
0.733 |
J |
0.395 |
|
Q |
1.628 |
Q |
0.443 |
|
Z |
3.441 |
M |
1.812 |
|
M |
3.834 |
P |
3.117 |
|
P |
4.355 |
Z |
3.402 |
|
R |
4.975 |
R |
3.478 |
|
A |
7.868 |
S |
5.712 |
|
S |
10.588 |
A |
7.760 |
|
O |
19.321 |
O |
13.415 |
|
It can be seen that the ascending orders of frequencies of C-characters in both Voynich-A and Voynich-B are rather similar, with only a few differences. Those differences could be expected since only two characters that are present in B disappear completely in A, while those characters (we will refer to them as V-characters) whose frequency drops in VMS-A as compared with VMS-B, still are present in A, albeit in much smaller numbers.
A similar picture is observed if we view the distribution of V-characters in both VMS-A and VMS-B texts. Namely, the order of frequencies of V-characters is almost the same in VMS-A and VMS-B, with a few minor differences.
These observations strongly point toward the notion that both VMS-A and VMS-B are written in the same language.
Overall, the relationship between the structures of Voynich-A and Voynich-B, in many respects, be it the total LSC sums, specific LSC sums, or characters frequency distribution variations, has many similarities to the relationship between all-letters and no-vowels versions of the previously tested meaningful texts in various natural languages.
I submit that all the listed facts are compatible with the hypothesis that VMS-A and VMS-B are written in the same language, the difference between them being in that text A uses a large number of abbreviations, substantially exceeding the number of abbreviations used in text B.
c. Abbreviated text in VMS-A?
First of all, the hypothesis of VMS-A and VMS-B being in the same language but differing in the degree to which abbreviated words have been used in each of those two parts of VMS, is well in agreement with the observation that the empirically estimated entropy of VMS-A, according to the data in Table 3, is considerably larger than it is for VMS-B. Indeed, if VMS-A is a highly abbreviated text, its redundance is substantially decreased, and therefore its entropy is larger.
Another fact being well in agreement with the assumption that VMS-A is a text with abundance of abbreviations is that the average length of a word in VMS-A is by about 35% shorter than it is in VMS-B.
There are two methods of abbreviation, abbreviation by truncation, and abbreviation by contraction. If word Professor is replaced with Prof, it is abbreviation by truncation. If word Mister is replaced by Mr it is abbreviation by contraction. In the former, vowels and consonants are sacrificed roughly equally. In the latter, vowels are sacrificed much more often than consonants are.
As I have mentioned, except for just two characters, 1 and 5, no other letter that is found in B is completely absent in A . This simply means that the alleged abbreviation was conducted not by consistently removing only vowels (as it was done in our no-vowels versions of previously tested texts), even though vowels must have been removed more often.
Here is an example. Let us try to abbreviate the following sentence: Ladies in that country wear long dresses and use cosmetics (the average word length in that sentence is 4.9 letters per word). Obviously, usually the first letter of each word would be preserved (therefore identical letters at the end/beginning of two consecutive words are preserved in the abreviated version -- in our case in VMS-A -- hence at n=1, the specific sums S/L* are almost equal for VMS-A and VMS B, as discussed earlier). If only vowels were removed in the abbreviation, word Ladies could be misunderstood (if converted to Lds, it can be interpreted as Lords, lands, lads, leads, etc). Hence, to preserve the meaning, the abbreviated version must keep some of the vowels, for example making it Ldis. Two vowels are sacrificed, but one is preserved. Word in probably would be preserved or replaced by a single symbol which by convention would mean in, for example, an analog of @, or the like. Word that may be abbreviated as tht since its reading would be assisted by context. Word country can become cntry, preserving y but removing the rest of the vowels. Word wear must preserve some vowels, for example becoming wer, hence losing one vowel, or maybe even remaining wear. Word long easily shrinks to lng, and dresses to drs or dres, losing a redundant second s. Word and probably would be replaced with a single symbol, like symbol & in English often is used. Word use would probably remain as it is, since us will be easily misconstrued, and se or simply s would be equally quite obscure. Finally, word cosmetics can safely reduce to csmtc, losing all vowels and one consonant as well. The result will be as follows: Ldis @ tht cntry wer lng dres & use csmtc. Instead of 49 letters in the full text, the abbreviated version contains only 32 symbols, having lost 12 vowels and 4 consonants, of which two have been replaced by different symbols. The average word length in the abbreviated version is 3.2 letters per word, which is the decrease by 36%, hence it is quite close to the observed difference in the average word length between VMS-A and VMS-B.
I submit that in Voynich-A the abbreviation was probably conducted mainly by contraction. Therefore, most of the C-characters, whose relative frequency in A is larger than it is in B, may be representing consonants, while most of V-characters may be representing vowels. Under this assumption, the probable consonants are, tentatively, as follows: O, S , A, R, P, M, Z, Q, J, *, W, D, I, T, Y, K, H, L, (total of 18 characters), and probable vowels (including possible diphtongs) or non-pronounced characters, tentatively, are C, 9, 8, E, F, 4, 2, N, 1, B, X, V, 3, U, 6, G, 0, 7, 5 (total of 19 characters). Obviosly, the number of characters allegedly representing vowels, which in the alphabets of most natural languages is below 15, seems to be too large to be true. On the other hand, the number of characters allegedly representing consonants seems to be too small (by some two to four characters). Hence the above tentative lists seem to need some corrections.
The corrections can be done, presumably, in two ways. First, obviously, in the process of abbreviation some consonants must have been sacrificed along with vowels, as it was in our example above. For such consonants, their frequency in VMS-A must become slightly lower than it is in VMS-B, but probably not to the same extent as for vowels. Reviewing the tables of character frequencies in A and B, we may assume that those characters whose frequency in A is just a little less than it is in B, probably are unfortunate consonants, which partially shared the fate of vowels, in the process of abbreviation. This assumption seems to be more probable in regard to the following characters: B, V, U. If we count these three characters among possible consonants, the total number of possible consonants increases to 21, while the number of possible vowels decreases to 16, which is not too different from what is found in some languages, like those that widely use diacritical marks, for example to distinguish between short and long vowels (as in Czech, where out of the total of 41 letters in the alphabet, 13 are vowels).
Second, as we discussed already, some of the characters in VMS may actually represent numerals. Under the second extreme assumption, namely that 10 least frequent characters in VMS represent numerals, the total number of characters representing letters would decrease from 37 to 27. Deleting from each of the tables of character frequencies for VMS-A and VMS-B, 10 least frequent characters and then repeating the manipulation of those tables, as done above (sorting out which characters are more frequent in A and which in B) I found, for these truncated tables, the following alternative lists of possiblle consonants and vowels. Possible consonants: O, A, S, R, Z, P, M, N, 1, B, X, Q, J, V, T, 3, *, U, W, and H (total of 20 characters). Possible vowels: C, 9, 8, E, F, 4, 2 (total of 7 characters).
Comment: It has been noticed [6] that there are certain words in VMS wich are common in VMS-A but very rare in VMS-B (for example 8AM) and some words (for example SC89 and ZC89) which are common in VMS-B but absent in VMS-A. If we accept the notion of VMS-A being written in a heavily abbreviated fashion, while VMS-B in a much less abbreviated one, then the above observation becomes easily explained. Namely, the described situation with word 8AM is then understood by assuming that the three-letter word in question is just some abbreviation, not unlike abbreviations LSC or VMS I have widely used in this paper. On the other hand words SC89 and ZC89 in VMS-B are "full" i.e. non-abbreviated versions which, when used in VMS-A are abbreviated to the extent to become unrecognizable as VMS-A versions of their full form in VMS-B. If I chose, in some parts of this paper, to use the non-abbreviated expressions Letter Serial Corellation instead of LSC and Voynich manuscript instead of VMS, then in such parts of the paper "words" LSC and VMS would be quite rare, or even completely absent, whereas they would remain common in the rest of the paper. On the other hand, the word Manuscript would happen regularly in the non-abbreviated parts of the paper but disappear in its abbreviated parts, becoming a part of the abbreviation VMS.
d) Vowels vs consonants in VMS
If we compare two lists, one based on the extreme assumption that all characters in VMS are letters, and the other based on the opposite extreme assumption that 10 least frequent characters are numerals, we see that there are a number of characters which in both lists are equally among either consonants or vowels.
Characters O, S, A, R, Z, P, M, Q, J, *, T, W, L and H, the total of 14 characters, under both extreme assumptions are listed among consonants. Since the actual situation is probably somewhere between the two extremes, these 14 characters may be counted as consonants with a reasonable confidence. Likewise, characters C, 9, 8, E, F, 4, 2, the total of 7 characters, under both opposite extreme assumptions, are listed as vowels, and therefore may be indeed considered to be vowels, with a reasonable confidence.
Comment. In [14] J. Reeds suggested a short list of possible vowels and consonants in VMS, based on considerations quite different from those I employed, as follows: Possible vowels O, 9, C, A, E; possible consonants 8 and S. If we compare J. Reeds' short lists with my more extensive lists, we see that characters 9, C, and E, which J. Reeds assumed to be vowels, in my list are also among vowels. However, characters O and A, which in J. Reeds' list are among vowels, in my list are counted among consonants. Character S, which J. Reeds listed as a posssible consonant, also in my list is supposedly a consonant. Character 8, which J. Reeds listed as a consonant, in my list is among vowels.
The above described division of characters in VMS into vowels and consonants is compatible with the fractions of vowels both in the alphabets and in the texts, which are normally found in natural languages. Indeed, two lists of possible vowels in VMS suggested above contain between 7 and 15 vowels, which means between about 19% and about 40 % of the alphabet. Since we have actually rejected the first, tentative list, we can maintain that the percentage of supposed vowels in VMS alphabet, as assumed above, is somewhere between 19% and 30 %, which is well within the normal range. As to the fraction of vowels in the text of VMS, accounting only for 7 vowels listed above, this fraction constitutes close to 40%, and even if we count all 15 tentatively assumed "vowels," this fraction is still not exceeding about 50%, which is again within the normal range for natural languages where this fraction is between about 38% for English and 62% for Finnish.
Of the rest of the characters in VMS (all of which are those that occur with a low frequency) seven characters, namely 1, B, X, V, 3, U, and N are, under one extreme assumption, listed as vowels, and under the opposite assumption, among consonants and therefore their nature remains ambiguous. Since the number of consonants in the alphabet must be substantially larger than 14, while the number of vowels may be close to 7, most of the seven uncertain characters more probably represent consonants. Ten least frequent characters, namely D, 6, G, 0, I, 7, 5, Y, K, and L appear only in the lists made up under the assumption that all characters in VMS are letters, since under the opposite assumption these characters are supposed to represent 10 numerals. Their exact meaning therefore also remains undefined, as some of them may indeed represent numerals, but some other, low-frequency letters.
6. CONCLUSION
As it was mentioned before, the described experimental observations, while having exluded a number of imaginable interpretations, give rise to two alternatives, to wit: a) VMS is a deliberately created highly organized gibberish, and b) VMS is a meaningful text in an unknown language which is characterized by an "abnormally" sharp non-uniformity of the letter frequency distribution.
While neither of the above two alternatives can be categorically proven or rejected on the basis of the experimental evidence presented in this paper, there is a certain asymmetry between the two explanations. Indeed, there are a number of arguments in favor of alternative b), but only one argument in favor of a) and against b). The latter is the above mentioned sharp non-uniformity of characters frequency distribution in both VMS-A and VMS-B, exceeding that in the twelve languages we studied. To review this non-uniformity, let us look at Fig. 21, where the standard criterion of distribution's uniformity, Coefficient of Variation, is shown for various languages, as well as for the artificial gibberish and for VMS.
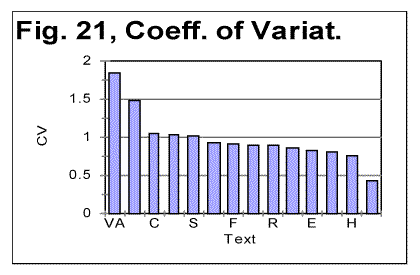
In Fig. 21 the peaks are in the following order (from left to right): VMS-A, VMS-B, Czech, German, Spanish, Greek, Finnish, Latin, Russian, Italian, English, Yiddish (in Latin characters) Hebrew, artificial gibberish. The peaks for both parts of VMS are for the versions assuming that all characters are letters. For all natural languages the peaks are for all-letters versions.
The graph in Fig. 21 shows that, whereas the Coefficient of Variation is indeed larger for both parts of VMS than it is for all meaningful texts in natural languages we studied, the step up from the peak for Czech, which is the largest of all peaks for the studied natural languages, to the peaks for VMS is not very drastic. Actually the ratio of CV for Czech to that for Hebrew is about the same as the ratio of CV for VMS to that for Czech. Under the assumption that 10 least frequent characters in VMS are numerals, the height of the peaks for VMS-A and VMS-B decreases, pushing them even closer to the heights of peaks for natural languages. This observation may possibly be viewed as attenuating the strength of the argument in favor of VMS being a highly organized gibberish, that argument being based on the "abnormally" high values of CV for VMS.
Furthermore, it seems hard to imagine that, however clever and skillful the creators of VMS could be, they would go to such lengths in their alleged imitation of a meaningful text, as to ensure the relative distributions of both vowels and consonants to be typical of natural languages, and also to imitate an abbreviated text. There would be no need whatsoever to effect the latter imitation. Therefore, based on the totality of the factual evidence, it seems more reasonable to conclude that 1) VMS is a meaningful text; 2) VMS-A and VMS-B are written in the same language, VMS-A constituting a version highly abbreviated by contraction. 3) The language of VMS has a very non-uniform letter frequency distribution (its entropy being though within the normal range for meaningful texts in 12 natural languages).
Also a seemingly reasonable identification of high-frequency characters representing either vowels or consonants has been suggested on the basis of the reported experimental data. If a natural (or artificial) language could be identified having the letter frequency distribution similarly non-uniform, with similar separate distributions of vowels and consonants, it would constitute a good candidate for reading VMS. The attempt to interpret VMS must be undertaken then on VMS-B first, to eschew additional difficulties posed by abbreviations.
Certainly, the above conclusions have not been proven beyond doubt, but just appear to be reasonable hypotheses compatible with the evidence presented.
As a final remark, I would like to point out that this paper leaves out many subtle features of VMS, including such observation as, for example, the signs that parts VMS-A and VMS-B consist, in their turn, of sub-parts, differing in certain characteristics (for example in the distribution of digrams, etc). The discussion of those subtle features of VMS can be found in many postings on the Web characterized by impressive sophistication and insights (see, for example [15]). Nevertheless, hopefully, this paper, although written by an amateur, may, in a small way, provide some additional glimpse into the mystery of VMS, and as such be somehow helpful as a small step toward the solution of that mystery.
Acknowledgments.
I would like to express my appreciation of the contribution by Dr. Brendan McKay (of Computer Science Department, Australia National University, Canberra, Australia). Dr. McKay has developed the computer program used for LSC tests, and conducted the measurements of LSC sums. He has also critically discussed with me the interpretation of LSC effect, in particular of its application to the Voynich manuscript. Of course the responsibility for any weaknesses of the interpretation in question is mine only.
1. D. Kahn, The Codebreakers, Weidenfeld and Nicolson Publishers, London, 1967.
2. W.R. Newbold, The Cipher of Roger Bacon. University of Pennsylvania Press, 1928.
3. http://www.borderlands.com/archives/arch/decipher.htm
4. http://home.att.net/~oko/home.htm
5. a) G. Landini, and R. Zandbergen, http://web.gham.ac.uj/G.Landini/evmt/evmt.htm ; b) Partial bibliography on Voynich manuscript: http://www.cla.ufl.edu/users/seeker1/fortpages/voynich-biblio.htm
6. P.H. Currier, http://Landau.phys.psu.edu/people/duvernois/currier.html
7. http://www.talkreason.org/marperak/Texts/Serialcor1.htm
8. http://www.talkreason.org/marperak/Texts/Serialcor2.htm
9. Text of the Voynich manuscript in Latin characters according to M. D'Imperio: http://Landau.phys.psu.edu/people/duvernois/voy.htm
10. http://www.talkreason.org/marperak/Texts/Serialcor3.htm
11. http://www.talkreason.org/marperak/Text/Serialcor4.htm
12. http://www.talkreason.org/marperak/Texts/addlang1.htm
13. http://www.talkreason.org/marperak/Texts/addlang2.htm
14. J. Reeds, http://www.research.att.com/~reeds/voynich/firth/05.txt
15. R. Zandbergen, http://www.geocities.com/Athens/Delphi/8956/curabcd.html .